Two Faces of Math

Math is the first place I remember feeling something bigger than myself, the first time I sensed the existence of patterns behind reality. Of some kind of truth.

The patterns I found in math were very simple, and very elegant. I’d stumble onto them unexpectedly, like taking a meandering path through the woods just to find myself back where I started but looking at it from the opposite end. Surprise, at first, followed quickly by – “oh, of course that’s how the path works. My simple human brain just wasn’t able to understand”.

Math worked the same way. You start with a few numbers. You do some simple calculations and get predictable results. You keep going, just doing some simple transformation or calculation at each step. Your mind is able to understand each step, but it’s hard to keep the whole picture in your head. And yet, still, patterns begin to emerge. You know you didn’t navigate yourself to them – you had no idea where you were going. You didn’t create them. It was more like they were there this entire time, and you just discovered them.

And a pattern that exists immortally, without every changing, well there’s only one word for it – truth. It is true in the purest sense – it doesn’t depend on anything to remain true. All life on Earth could end, but the Pythagorean theorem is still true. It’s just a pattern built into the concept of a triangle, waiting for anyone who asks the right question to come discover it.

I remember the multiple proofs the Pythagoreans came up with for their startling discovery. My favorite was a geometric one: the square of their sides is equal to the area of a square that extends from that base.

For the Pythagoreans, the beauty of their namesake theory was literally spiritual. They were more than a group of mathematicians in Ancient Greece. They were a pseudo-religious cult. The beauty of the truth of their theory impressed them so much that they felt they had found the divine in numbers.

The Greeks were not the only ones. A thousand years later, in the deserts of the Arabian peninsula, the new religion of Islam shunned idols and adopted the symbols of geometry instead to represent their god Allah. Their mathematicians were also their religious scholars, passing on to the West the basis of modern-day arithmetic and algebra (the word itself “al-gebra” from Arabic).

Before school knocked the love out of me, math was something I adored. It was not a series of techniques that yield the Right Answer that some authority figure was looking for. It was the study of elegance. Any time I got confused, or math seemed complicated, it was because of the complications that I had brought to the table. The problem was simple, if viewed from the right perspective. It was me who was muddying it up by looking at it all upside down.

Polar coordinates were one of those moments for me. Growing up, we’re used to seeing graphs with x and y coordinates. To tell someone where a point on the graph is, you tell them how far to go along the horizontal axis (the x coordinate) and then, from there, how far to go up in the vertical direction (the y coordinate). Lots of things can be explained easily this way, like a live, which just changes its y-coordinate in proportion to its x-coordinate. But other things are a lot harder to reason about in this way.

Like a circle. In our traditional x-y graph, the equation for a circle is something unwieldly, like x^2 + y^2 = 1. It’s hard to understand how to even begin to plot that on a coordinate grid.

It’s hard only because of the way we decided to look at the problem. Because of the type of coordinates we chose. The real thing that we’re trying to express here isn’t a bunch of x-coordinates and y-coordinates. They’re just a means to get to our real ends – a series of points that together make up a shape and have a certain relationship.

So we can pick another way to represent points. Such as “I’ll tell you the direction to walk as an angle from the origin at the center of the graph, and I’ll tell you the distance to go.”

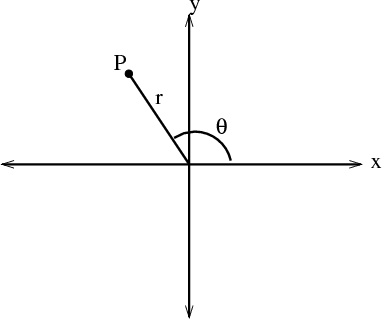
What we would have earlier called “Go up 1 on the y-axis” is now just “Go 1, in the 90 degree direction”. Simple enough. It seems like the same thing. But the magic starts happening when you describe round shapes.

A circle is just “stay a fixed distance from the origin. Start at 0 degrees and walk all the way around”. That’s a lot simpler of an explanation than x^2 + y^2 = 1!

This kind of elegance from a simple perspective shift comes up in math over and over again. What was once a complicated problem seems to collapse on itself. All the complexity suddenly gets sucked out, and the solution is right there staring you in the face.

Mathematicians often talk about a-ha moments. Keith Devlin, a math professor at Stanford, describes the experience: “It’s the insight. It’s the a-ha moment…often mathematics proceeds by ‘no idea, no idea, no idea’ and then suddenly ‘oh! A great idea!”

Patters that already exist. A sense of discovery. A feeling of elegance in the conclusions. This is enough to leave a grown adult in awe. Just imagine what it would do on a child.

Math introduced me to the idea that truths exist outside of me, that there is a pattern to the Universe, and if we peer into it at just the right angle, we can glimpse the brilliance of some inner, indescribable truth.

I was lucky. I got to experience this before school drilled math into me as a boring, practical tool. We are told math is a way to solve equations, not a way to discover beauty and truth. It is eminently practical, couched in word problems about every day situations. Exchanging apples, or comparing prices at the grocery store. We are told we must learn it because how could we live without it.

If math was the source of our industrial religion, we worship it today with all the wisdom of a rote ritual, with incantations in a language we don’t understand and steps we assiduously follow, lest the magic cease to work. We are kept from asking questions about this, shushed when we wonder out loud “yes it works, but why”. Because we have taken the true god of creativity and turned him into the false prophet of practicality, and now we dance around pouring milk on his head and praying for it to give us our solutions.

What most kids experience from math is how to do it wrong. For them, it’s just some ritual imposed by the powers that be, and the best they can hope for is to escape without getting slapped on the wrist. All that matters is getting the Right Answer, not your conceptual understanding of the ideas themselves. Do you understand division as the inverse of multiplication? Great. But if you mess up in your long division of 204 by 17, it doesn’t matter what you conceptually understand. You still get a 0.

This doesn’t end in 6th grade, or 8th grade, or even after 12th grade. It continues into college and well beyond. Do you understand that eigenvectors are a reorientation of your vector space into mutually orthogonal bases? That it is the cleanest way to represent the relationships inherent in your particular system? Great, you get it, but if you can’t calculate the determinant by hand, if you don’t arrive at the right numbers, at the Right Answer, it doesn’t matter what you understand. You don’t get the grade.

Part of this deficiency is purely logistical. It’s easier to test someone by asking a question and checking if their answer matches an expected output, number for number or word for word. It is hard to scale testing or keep it free from bias, when you have to try to subjectively assess whether someone understands something or not. One is easy and explicit. The other is a judgement call.

But in the decades of post-war, modern education, we have barely even tried. Lots of educators have had lots of ideas about how to change the way we teach our kids. Many of these ideas try to return education to its roots. None of them have taken off. Our form of education today is only marginally different than what we’ve had for many generations. For a world that is constantly improving and innovating in every field, education is a glaring laggard. Why?

The truth is we don’t care to fix it. The truth is that while we pay lip service to the “value of education,” we are happy to have it be a selection mechanism, not a way to nurture young minds. We are fine with the fact that tests measure conformity, that our system extinguishes creativity, that we produce human beings stripped of individuality, ready to do the bidding of the day – be it spreadsheets or slides or documents – reliably, efficiently, without complaint.